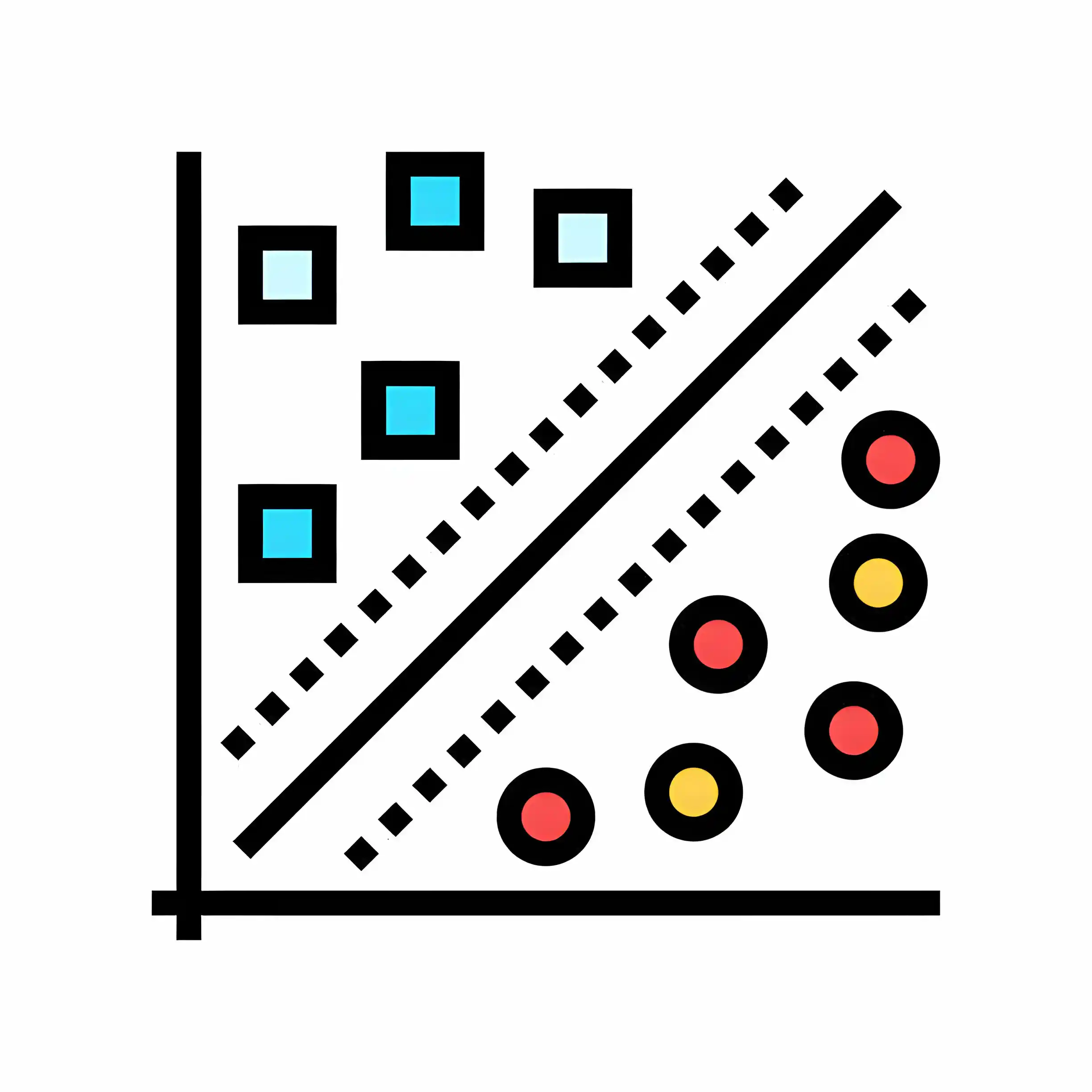
A Support Vector Machine (SVM) is particularly well-suited for classification problems where the data is linearly separable or can be transformed into a higher-dimensional space where it becomes separable.
Here’s a brief overview of how SVM works:
- Linear Separability: Given a set of labeled data points, SVM aims to find the hyperplane that best separates the classes. In a binary classification scenario, this hyperplane is a line in two dimensions, a plane in three dimensions, and a hyperplane in higher dimensions.
- Maximizing Margin: SVM aims to maximize the margin, which is the distance between the hyperplane and the nearest data points from each class. These data points, known as support vectors, are crucial in defining the decision boundary. By maximizing the margin, SVM tends to generalize better to unseen data.
- Kernel Trick: In cases where the data is not linearly separable in its original feature space, SVM can employ a kernel trick to map the data into a higher-dimensional space where it becomes separable. Common kernels used include the linear kernel, polynomial kernel, Gaussian (RBF) kernel, and sigmoid kernel. The choice of kernel depends on the nature of the data and the problem at hand.
- Regularization: SVM incorporates a regularization parameter (C) that controls the trade-off between maximizing the margin and minimizing classification errors. A smaller C value allows for a larger margin but may lead to misclassification errors, while a larger C value emphasizes classification accuracy at the expense of a narrower margin.
- Classification: Once the optimal hyperplane is determined during training, SVM can be used for classification by evaluating which side of the hyperplane new data points fall on. The decision boundary is typically defined by a threshold value, and points above the threshold belong to one class while points below it belong to the other class.
SVMs are widely used in data science for classification tasks, especially when dealing with small to medium-sized datasets. They have advantages such as high accuracy, robustness against overfitting, and effectiveness in high-dimensional spaces. However, they can be sensitive to the choice of parameters and require careful tuning, especially when using nonlinear kernels. Additionally, SVMs might not perform well on very large datasets due to their computational complexity.